Функция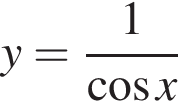 
не определена в точке:
1) 
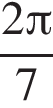
2) 
3) 
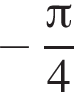
4) 
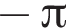
5) 
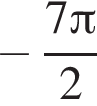
Решение. Функция 
не определена, когда 
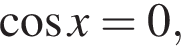т. е. при 
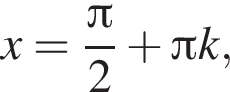где 
Таким образом, она не определена в точке 
Правильный ответ указан под номером 5.
Ответ: 5
331
5
Сложность: I
РЕШУ ЦТ — математика
Вариант № 466
1.
i
Функция 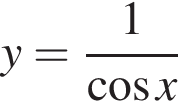не определена в точке:
1)
2)
3)
4)
5)
2.
i
Пусть O и O1 — центры оснований цилиндра, изображенного на рисунке. Тогда образующей цилиндра является отрезок:
1) DB
2) DC
3) DO1
4) OO1
5) AD
3.
i
Если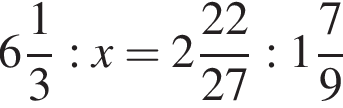 
— верная пропорция, то число x равно:
1) 
2) 
3) 
4) 
5) 
4.
i
Найдите значение выражения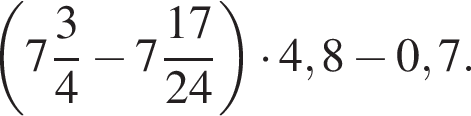 
1) 0,5
2) 0,9
3) −0,9
4) −0,5
5) 2,4
5.
i
Если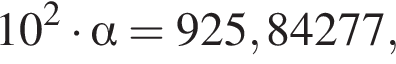 
то значение α с точностью до сотых равно:
1) 9,25
2) 92,58
3) 9,26
4) 92584,28
5) 9258,43
6.
i
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что
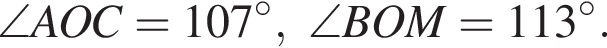Найдите величину угла BOC.
1) 
2) 
3) 
4) 
5) 
7.
i
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 5x + 3 = 0. Найдите площадь треугольника.
1) 5
2) 4
3) 3
4) 2,5
5) 1,5
8.
i
Расположите числа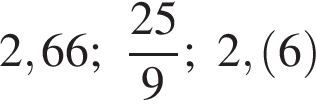 
в порядке возрастания.
1) 
2)
3) 
4) 
5) 
9.
i
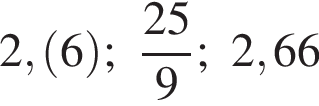
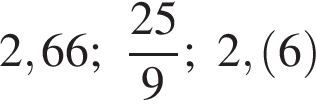
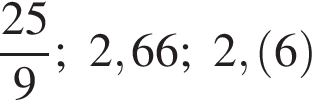
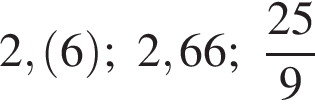
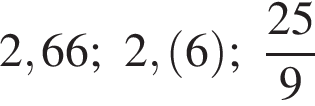
Найдите значение выражения НОК(12, 18, 36)+НОД(39,52).
1) 26
2) 50
3) 48
4) 72
5) 49
10.
i
Площадь осевого сечения цилиндра равна 36. Площадь его боковой поверхности равна:
1) 
2) 
3) 
4) 
5) 
так как это прямоугольник. Тогда для площади боковой поверхности имеем:
11.
i
Упростите выражение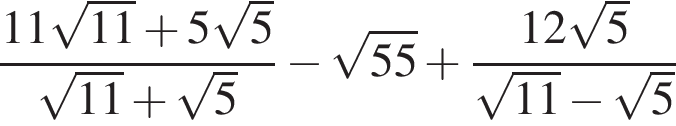 
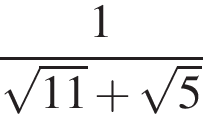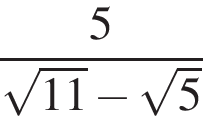1) 
;
;2) 
;
;3) 
;
;4) 
;
;5) 
.
.
12.
i
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 20 кг свежих.
1) 
2) 
3) 
4) 
5) 
13.
i
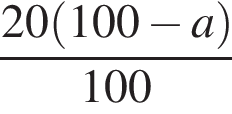
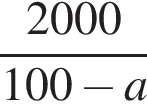
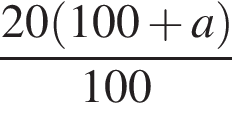
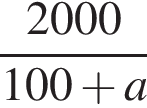
Найдите длину средней линии прямоугольной трапеции с острым углом 60°, у которой большая боковая сторона и большее основание равны 16.
1) 24
2) 8
3) 12
4) 
5) 
поэтому 
14.
i
Упростите выражение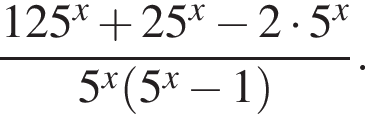 
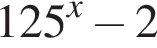
1) 
2) 
3) 
4) 
5) 
тогда дробь примет вид: 
Тем самым, исходное выражение равно 
15.
i
Количество целых решений неравенства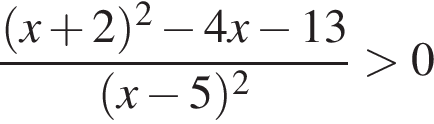 
на промежутке 
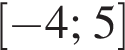равно:
1) 3
2) 5
3) 4
4) 2
5) 7
Корни знаменателя 
кратности 2:
Следовательно, существует только 2 целых решения. 16.
i
В ромб площадью 
вписан круг площадью 5π. Сторона ромба равна:
1) 8
2) 4
3) 
4) 
5) 16
Следовательно, радиус круга равен: 
Площадь ромба равна произведению высоты на его сторону: 
Тогда: 
17.
i
График функции, заданной формулой y = kx + b, симметричен относительно оси Oy и проходит через точку A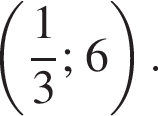
Значение выражения k + b равно:
1) 
2) 
3) 
4)
5) 
Прямая проходит через точку A с координатами 
отсюда b = 6. Поэтому k + b = 6.18.
i
Найдите наименьший положительный корень уравнения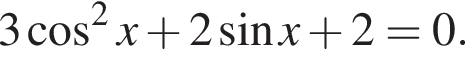 
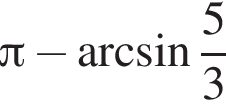
1) 
2) 
3) 
4) 
5) 
получим: 
Сделаем замену 
Решим уравнение:
или 
Первое уравнение решений не имеет, поскольку 
Рассмотрим второе уравнение: 
он указан под номером 4.19.
i
Если в правильной четырехугольной пирамиде высота равна 3, а площадь диагонального сечения равна 9, то ее объем равен ...
следовательно, 
Следовательно,
20.
i
Решите уравнение 
В ответ запишите сумму его корней (корень, если он один).
21.
i
В окружность радиусом 6 вписан треугольник, длины двух сторон которого равны 6 и 10. Найдите длину высоты треугольника, проведенной к его третьей стороне.
откуда 
Из прямоугольного треугольника BHC имеем:
22.
i
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна 
раз больше его стороны. Поэтому сторона равна 11, периметр — 66.23.
i
Найдите наибольшее целое решение неравенства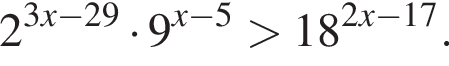 
:
24.
i
Найдите количество корней уравнения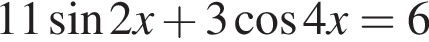 
на промежутке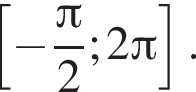 
Тогда:
4 корня.25.
i
Четырёхугольник ABCD вписан в окружность. Если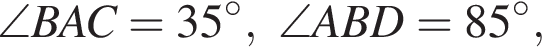 
то градусная мера между прямыми AB и CD равна ...
26.
i
Найдите количество корней уравнения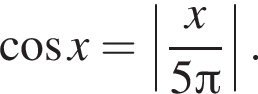 
уравнение не имеет корней. На отрезке 
уравнение будет иметь 2 корня. Заметим, что на каждом из отрезков 
вплоть до 
уравнение будет иметь два корня. На отрезке 
уравнение будет иметь 1 решение в силу того, что в точке 
решений нет. Поэтому на положительной полуоси уравнение имеет 5 решений. В силу четности левой и правой частей уравнения всего имеем 10 решений.27.
i
Найдите сумму целых значений x, принадлежащих области определения функции
28.
i
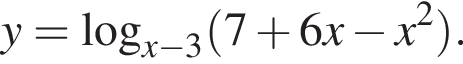
В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен 
Найдите 18sinβ, где β — угол между диагональю трапеции и плоскостью α.
Поскольку все стороны трапеции, кроме большего основания равны a, получим 
Тогда 
: 
29.
i
Из двух растворов с различным процентным содержанием спирта массой 450 г и 300 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
во втором — 
После переливания масса спирта в 1-ом сосуде равна 
во втором — 
Так как концентрации стали одинаковыми, а объёмы относятся как 3:2, во втором сосуде в 1,5 раза меньше спирта. Тогда:
Тогда 
30.
i
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал 
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 12.
времени на выполнение всей работы, в то время, как первый за 
работы. 
времени на выполнение всей работы, в то время, как второй за 
работы. 
времени на выполнение всей работы, в то время, как третий за 
работы. 
то они выполнили бы работу за: 
Поэтому, работая вместе работа была бы выполнена в 
раза быстрее. В ответе будет число 